反向删除算法的目的是通过删除高权重的边来找到最小生成树,其算法逻辑是,先对加权图所有的边进行降序排列,从最高权重的边开始执行删除操作,如果删除该边不影响加权图连接,则删去这条边并继续删除筛选;如果删除该边会影响加权图链接,则恢复保留删除的边,继续删除筛选。直至遍历完所有的边,最后就能输出最小生成树。
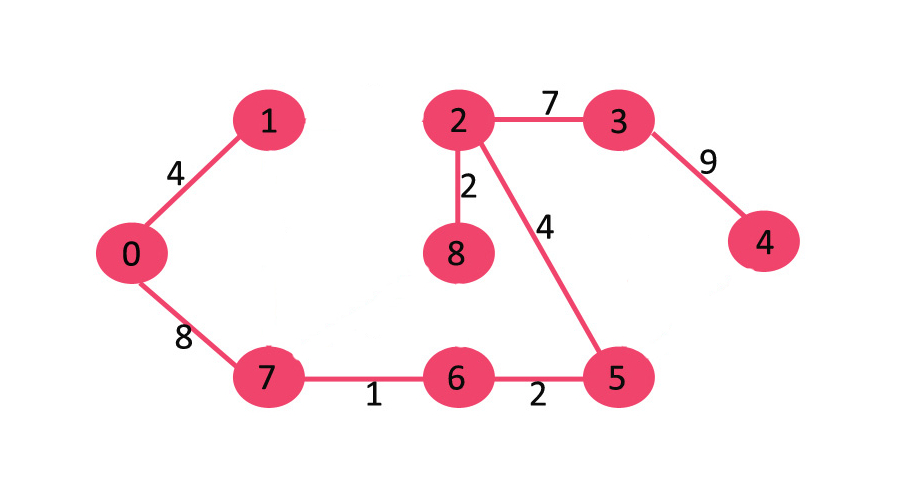
反向删除算法输出最小生成树实例
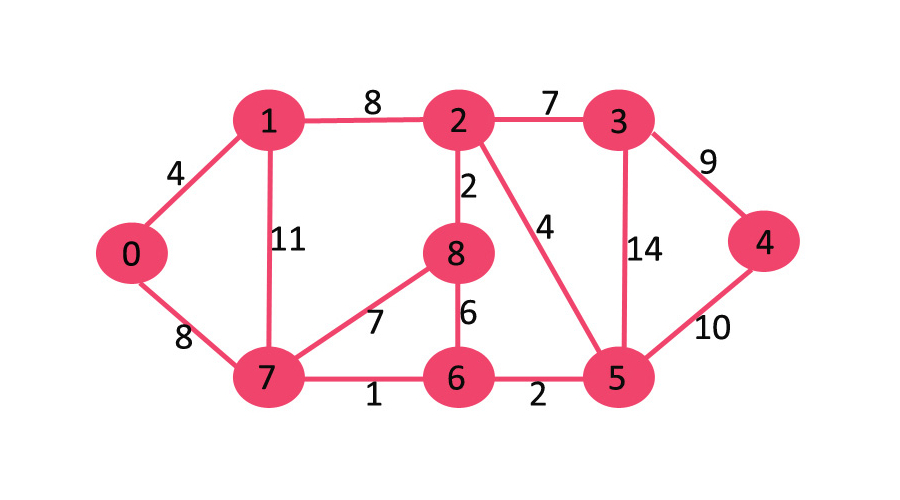
上述加权图为初始图,根据反向删除算法,先删除权重为14的最高权重边,因加权图不会断开连接,因此将其删除。
接下来删除权重边11,删除它不会断开加权图,将其删除;
接下来删除权重边10,删除它不会断开加权图,将其删除;
接下来删除权重边9,删除后会导致加权图断开连接,因此保留权重边9;
接下来删除权重边8,因为权重边8有2条,在权重边缘相同的情况下,我们可以选择相同权重边缘的任何边缘。这里我选择边(0,7);
接下来删除权重边7,因为权重边7有2条,这里我选择边(2,3);
接下来删除权重边6,删除它不会断开加权图,将其删除;
接下来删除权重边4,删除后会导致加权图断开连接,因此保留权重边4;
接下来删除权重边2,删除后会导致加权图断开连接,因此保留权重边2;
接下来删除权重边1,删除后会导致加权图断开连接,因此保留权重边1;
至此,已经遍历完所有的边,输出得到最小生成树,如下图: