Kruskal算法是最小生成树的流行算法之一,以生成局部最优解的形式查找最小生成树。Kruskal算法将图视为森林,每个节点视为单独的树,并且只有在与所有其他可用选项相比成本最低的情况下,才将一个节点与另一个节点连接起来。
Kruskal算法的步骤原理
1、根据权重对图边进行排序,从权重最小的边开始
2、选择最小的边,检查它是否与现有生成树形成循环,如果有将这条边加入生成树中,如果没有生成循环,则舍弃。
3、重复步骤2,直到生成树中有(V-1)条边,最后的生成树即为最小生成树
Kruskal算法图解
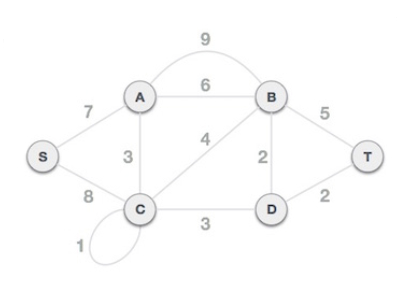
第1步,删除所有循环和平行边
从给定图中删除所有循环和平行边
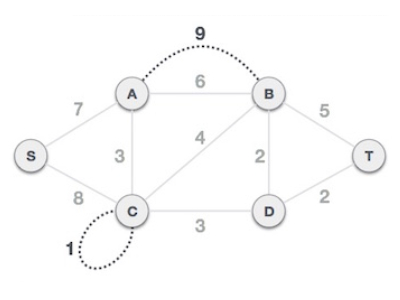
在平行边的情况下,保留相关成本最低的边并删除所有其他边。
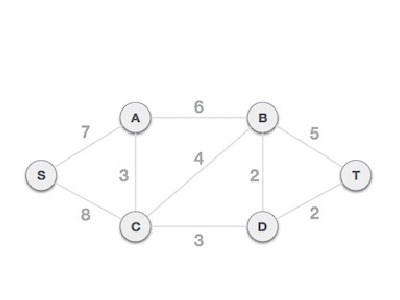
第2步,按权重递增的顺序排列所有边
下一步是创建一组边和权重,并按权重(成本)的升序排列它们

第3步,添加权重最小的边
现在我们从权重最小的边开始向图中添加边。在整个过程中,我们将继续检查跨越属性是否完好无损。如果通过添加一条边,生成树属性不成立,那么我们将考虑不将边包括在图中。
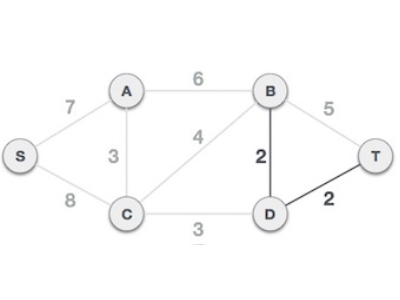
最小成本是2,涉及的边是B,D和D,T。我们添加它们。添加它们不会违反生成树属性,因此我们继续进行下一个边选择。
下一个成本是3,关联的边是A,C和C,D。我们再次添加它们。
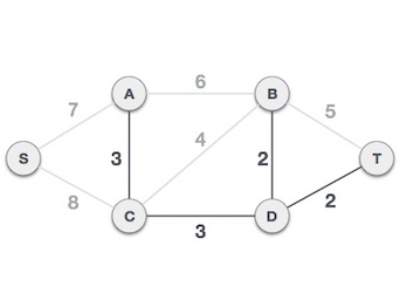
表中的下一个成本是4,我们观察到添加它会在图中创建关联边。
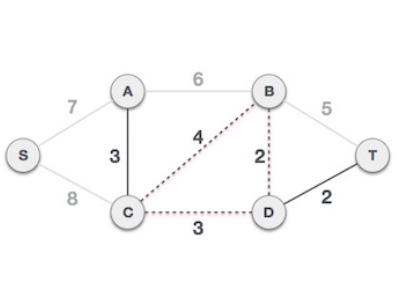
在此过程中,我们将忽略/避免创建4的所有边缘。

观察到成本为5和6的边也会创建关联边。我们忽略它们并继续。
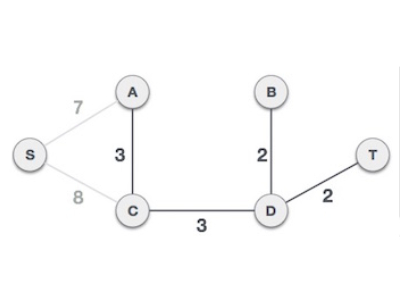
现在只剩下一个要添加的节点了。在两个可用的最低成本边7和8之间,添加成本为7的边。
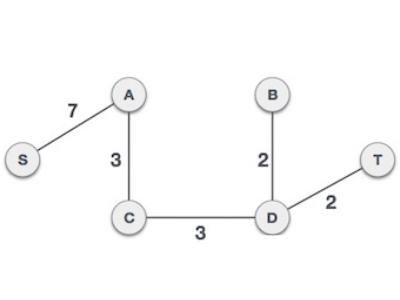
最后添加边S,A,此时已经包含了图的所有节点,现在就是最小成本生成树。




