Ford-Fulkerson算法是贪心算法,用于计算网络中的最大流量。其原理是找到剩余容量为正的增广路径,只要找到增广路径,就可以继续增加路径和计算流量。直到增广路径不再存在,这时就能得出最大流量。
Ford-Fulkerson算法的术语
剩余容量:就是将容量减去流量,在Ford-Fulkerson算法中剩余容量是正数,才能继续作为路径。
残差网络:是一个具有相同顶点和边的网络,使用残差容量作为容量。
增广路径:是残差图中从源点到接收点的路径,最终容量为0。
Ford-Fulkerson算法原理示例
可能概念不是很清晰,下面来看一个示例,流网络所有边的初始流量均为0,并有对应的容量上限,设起始点为S,接收点为T。
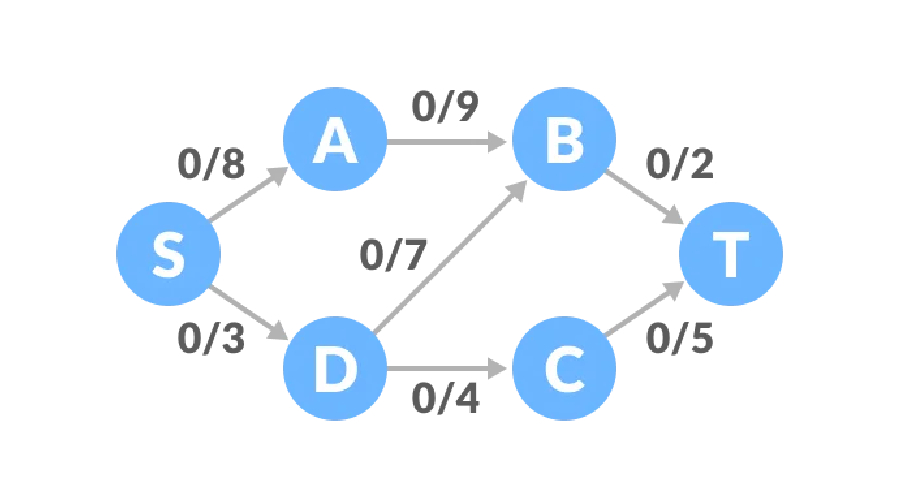
路径一,S-A-B-T路径剩余容量为8、9、2,最小值为2,因此路径一的流量为2,这时网络图的流量为2。
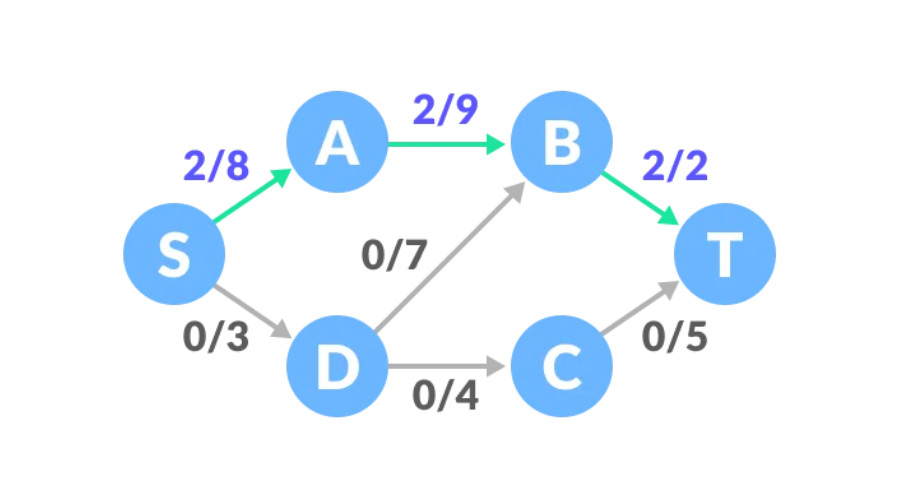
路径二,S-D-C-T路径剩余容量为3、4、5,最小值为3,因此我们可以将流量增加3,这时网络的流量为5。
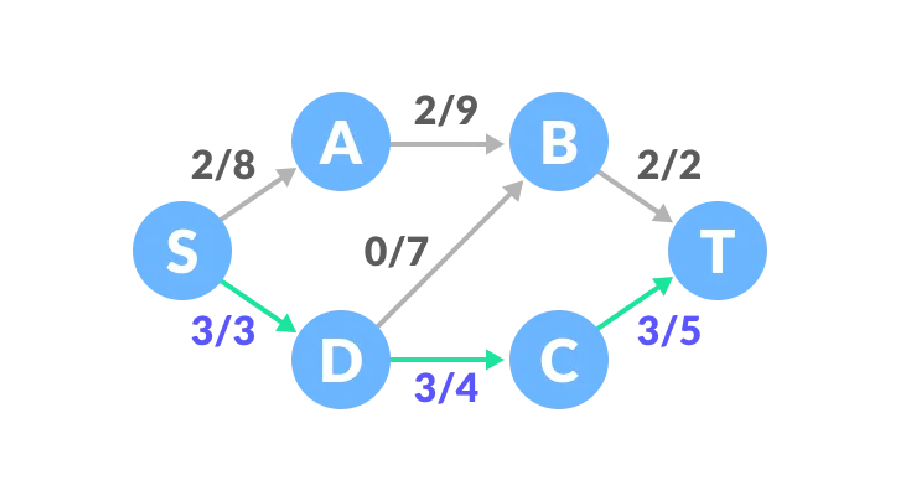
路径三,S-A-B-D-C-T路径剩余容量为6、7、7、1、2,最小值为1,因此流量增加1,这时网络的流量为6。
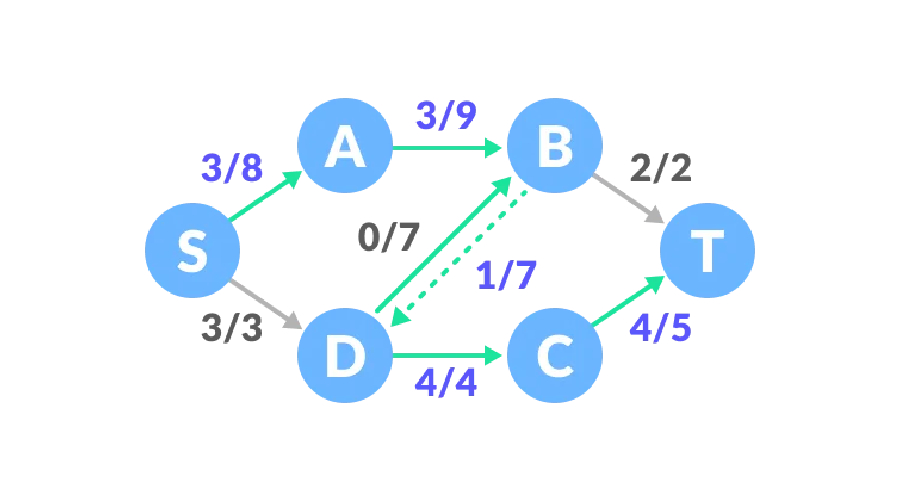
至此,已经没有为正数的剩余容量,得出该流网络的最大流是6。
Python实现Ford-Fulkerson算法
from collections import defaultdict
class Graph:
def __init__(self, graph):
self.graph = graph
self. ROW = len(graph)
def searching_algo_BFS(self, s, t, parent):
visited = [False] * (self.ROW)
queue = []
queue.append(s)
visited[s] = True
while queue:
u = queue.pop(0)
for ind, val in enumerate(self.graph[u]):
if visited[ind] == False and val > 0:
queue.append(ind)
visited[ind] = True
parent[ind] = u
return True if visited[t] else False
def ford_fulkerson(self, source, sink):
parent = [-1] * (self.ROW)
max_flow = 0
while self.searching_algo_BFS(source, sink, parent):
path_flow = float("Inf")
s = sink
while(s != source):
path_flow = min(path_flow, self.graph[parent[s]][s])
s = parent[s]
max_flow += path_flow
v = sink
while(v != source):
u = parent[v]
self.graph[u][v] -= path_flow
self.graph[v][u] += path_flow
v = parent[v]
return max_flow
graph = [[0, 8, 0, 0, 3, 0],
[0, 0, 9, 0, 0, 0],
[0, 0, 0, 0, 7, 2],
[0, 0, 0, 0, 0, 5],
[0, 0, 7, 4, 0, 0],
[0, 0, 0, 0, 0, 0]]
g = Graph(graph)
source = 0
sink = 5
print("Max Flow: %d " % g.ford_fulkerson(source, sink))



