深度学习是机器学习的一个分支,它基于大脑在数据处理中的能力。目的是在大脑中创建神经网络模型,并为问题提供解决方案。通过这种方式,它允许机器在没有人类监督的情况下学习。为此,它使用人工神经网络。
要了解神经网络的功能,可以考虑神经元中的脉冲传输。从树突末端接收到的数据在细胞核中加权(乘以w)并沿着轴突传输并连接到另一个神经细胞。从一个神经元出来的轴突(x's)成为另一个神经元的输入。这样就保证了神经之间的传递。
为了在计算机上对其进行建模和训练,我们需要知道这个操作的算法,也就是说,我们需要能够通过对输入应用一系列命令来获得输出。
这里我们通过数学来表达,具体如下:
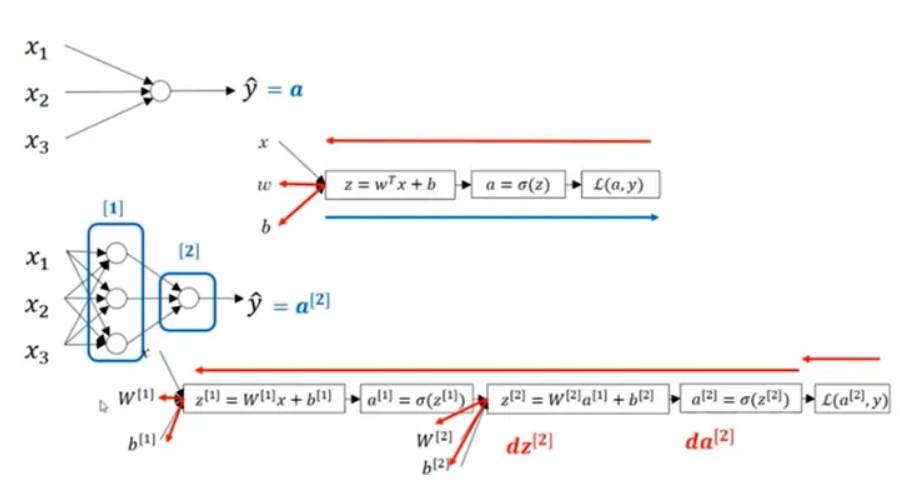
图中的数值[1]和[2]代表层数,可以看到上面是单层网络结构,下面是简单的多层网络结构(加1变成了2层隐藏层)。
x输入值乘以w权重,w权重在开始时被赋予随机值,偏差被添加得到z值,这个值在公共节点中有一个值。通过激活函数获得的a值成为我们的输出,并且此a值受到具有所需y值的损失函数的影响。
然后我们通过反向传播,返回并在相反的方向上做所有的工作,通过导数向后移动并记下获得的值。新的权重值在此过程中变得很重要,这些新的权重值会被再次使用。然后继续这个过程,直到损失收敛到最小值并找到最佳模型,这个过程被称为前馈反向传播算法。
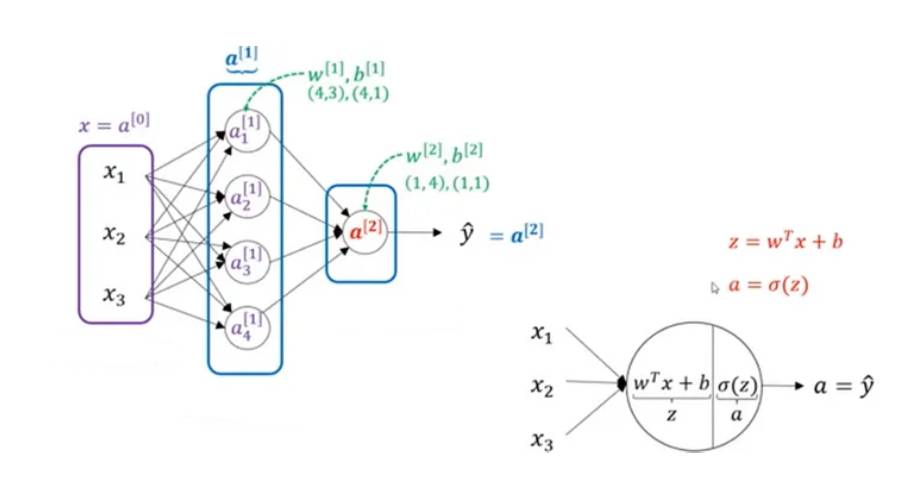
在上图中,可以看到一个2层神经网络,一个包含4个神经元的隐藏层和一个包含单个神经元的输出层。输入层对层数没有影响。这些值表示为w(其层中的神经元数量,输入值的数量)和b(其层中的神经元数量)。隐藏层的输入是x,输出层的输入是a的值。
双曲正切、ReLU、Leaky ReLU等都能代替sigmoid函数作为激活函数,这些函数在层中使用,并且必须是可微的。因为我们通过反向传播中的导数操作来更新权重。
ReLU激活函数在深度学习中使用最多。由于小于0的部分在ReLU中不可微,因此它们不能参与该过程并且该部分不会发生学习。小于0的值在Leaky ReLU中也是可微的,并且由于每个值都有一个结果,因此在任何情况下都会进行学习。






