DFS算法概念原理详细图解 Python代码实现DFS算法

DFS算法又名深度优先搜索，作为递归算法，通过堆栈，在避免循环的同时遍历目标所有节点。

DFS算法的工作原理图解

以具有5个节点的无向图为例，如下图：

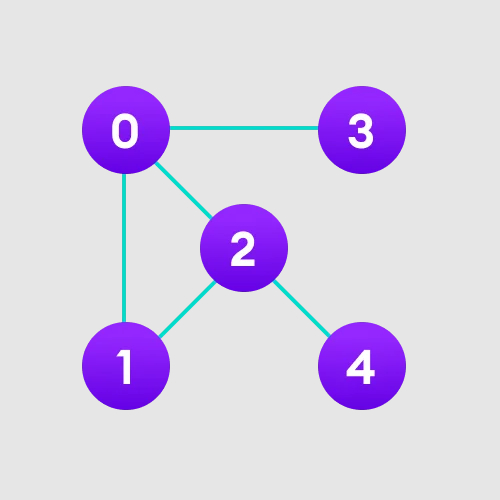
从节点0开始，DFS算法首先将其放入Visited列表并将其所有相邻顶点放入堆栈。

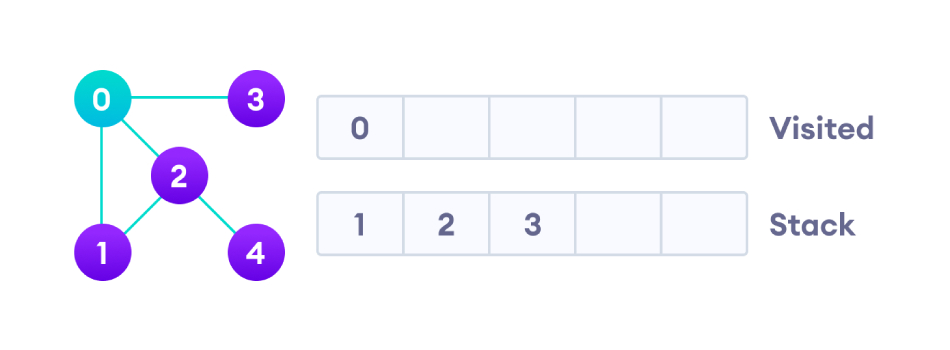
接着，访问堆栈顶部的节点1，并转到其相邻节点。因为0已经被访问过，所以访问2。

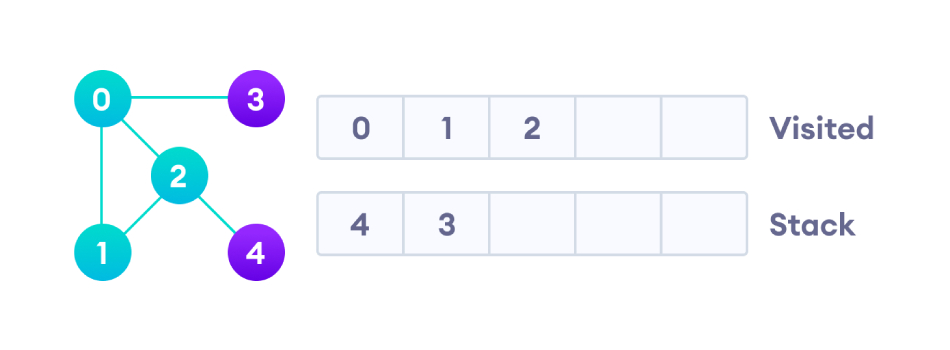
节点2有一个未访问的相邻节点4，因此我们将其添加到堆栈顶部并访问它。

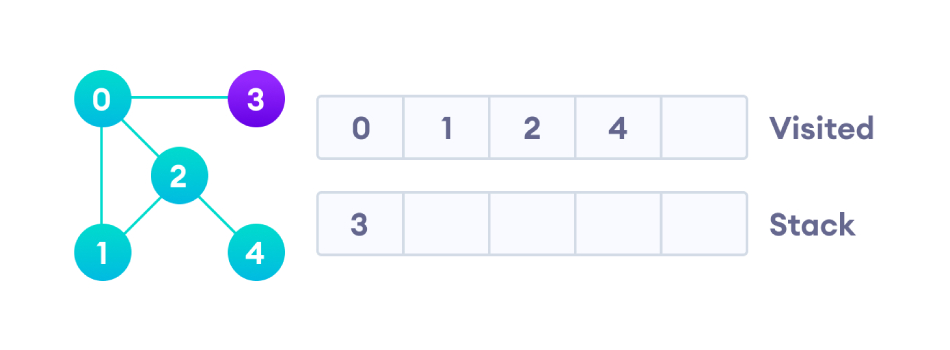
现在，还有最后一个节点没有访问，我们继续往下。在最后访问3之后，已经没有还未访问的相邻节点，因此我们完成了该无向图的深度优先遍历。

DFS算法伪代码

在init()函数中，请注意我们在每个节点上运行DFS函数。这是因为图可能有两个不同的不连贯部分，因此为了确保覆盖每个顶点，我们还可以在每个节点上运行DFS算法。

DFS(G, u)
    u.visited = true
    for each v ∈ G.Adj[u]
        if v.visited == false
            DFS(G,v)
init() {
    For each u ∈ G
        u.visited = false
     For each u ∈ G
       DFS(G, u)
}

Python代码实现DFS算法

def dfs(graph, start, visited=None):
    if visited is None:
        visited = set()
    visited.add(start)

    print(start)

    for next in graph[start] - visited:
        dfs(graph, next, visited)
    return visited

graph = {'0': set(['1', '2']),
         '1': set(['0', '3', '4']),
         '2': set(['0']),
         '3': set(['1']),
         '4': set(['2', '3'])}

dfs(graph, '0')