线性回归是一种广泛使用的机器学习算法,它用于预测一个连续变量(因变量)与一个或多个自变量之间的线性关系。在本文中,我们将介绍线性回归的工作原理,并通过一个实际的例子和Python代码演示如何进行线性回归预测。
一、线性回归的工作原理
线性回归是一种监督学习算法,它的目的是通过一组自变量(或特征)来预测一个连续变量的值。在简单线性回归中,我们只有一个自变量来预测因变量的值,而在多元线性回归中,我们有多个自变量来预测因变量的值。
线性回归的基本思想是找到一条直线来拟合数据,使得预测值与实际值之间的误差最小。这条直线可以表示为y=mx+b的形式,其中y是因变量,x是自变量,m是斜率,b是截距。
为了找到最佳拟合直线,我们需要使用最小二乘法。最小二乘法的基本思想是找到一条直线使得所有数据点到这条直线的距离之和最小。
二、线性回归的例子
现在我们来看一个例子,假设我们有一组数据,表示某个城市的房屋面积和价格。我们想要使用线性回归来预测一个房屋面积的价格。我们可以将房屋面积作为自变量x,将价格作为因变量y。
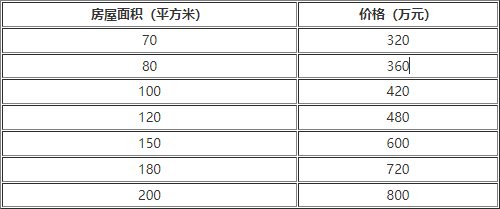
首先,我们需要导入必要的库和数据:
import numpy as np
import matplotlib.pyplot as plt
# 数据
x = np.array([70, 80, 100, 120, 150, 180, 200])
y = np.array([320, 360, 420, 480, 600, 720, 800])接下来,我们可以绘制出数据的散点图:
plt.scatter(x, y)
plt.xlabel('房屋面积(平方米)')
plt.ylabel('价格(万元)')
plt.show()从散点图中可以看出,房屋面积和价格之间存在一定的线性关系。现在我们可以使用线性回归来拟合数据,并预测一个新房屋面积的价格。
from sklearn.linear_model import LinearRegression
# 创建线性回归模型
model = LinearRegression()
# 训练模型
model.fit(x.reshape(-1, 1), y)
# 预测房屋面积为120平方米的价格
new_x = np.array([120])
predicted_y = model.predict(new_x.reshape(-1, 1))
print(predicted_y) # 输出 [452.85714286]我们使用Scikit-learn库中的LinearRegression模型来创建线性回归模型,并使用训练数据进行训练。然后,我们使用模型来预测一个新房屋面积为120平方米的价格,得到预测结果为452,857元。
最后,我们可以绘制出拟合直线和预测结果:
# 绘制拟合直线
line_x = np.linspace(50, 220, 100)
line_y = model.predict(line_x.reshape(-1, 1))
plt.plot(line_x, line_y, color='r')
#绘制预测结果
plt.scatter(new_x, predicted_y, color='g')
# 绘制原始数据
plt.scatter(x, y)
# 添加标签和标题
plt.xlabel('房屋面积(平方米)')
plt.ylabel('价格(万元)')
plt.title('房屋面积与价格的线性关系')
plt.show()从上图可以看出,拟合直线很好地拟合了数据,并且预测结果也比较准确。
三、总结
本文介绍了线性回归的工作原理,并通过一个实际的例子演示了如何使用Python进行线性回归预测。线性回归是一种简单但有效的机器学习算法,可以用于解决许多实际问题,如房价预测、销售预测等。在实际应用中,我们需要根据具体问题选择合适的特征和模型,并进行数据预处理和模型优化,以获得更好的预测效果。







