红黑树的原理和特性 Python代码实现红黑树

红黑树和B+树一样，是平衡二叉搜索树。红黑树每个节点都是有颜色的，要么是红色，要么黑色，但树的根是黑色，最底部的叶也是黑色的。还需要注意的是，红黑树任何节点到叶的直接路径包含相同数量的黑色节点。

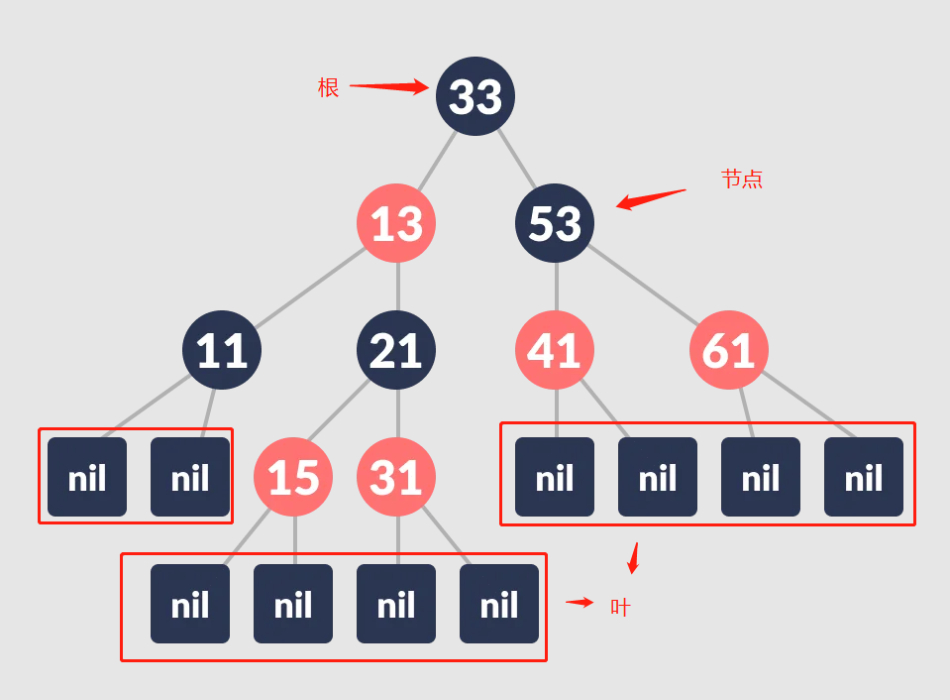
红黑树如何保持自平衡的特性？

红黑树节点颜色的限制确保从根到叶的最长路径不超过最短路径的两倍。

为什么新插入的节点在红黑树中总是红色的？

这是因为插入红色节点不会违反红黑树的黑色节点数量性质。而且即便是新增红色节点插入到原本的红色节点，解决此问题会比违反黑色节点引起的问题更加容易。

红黑树Python代码实现

import sys
# 创建节点
class Node():
    def __init__(self, item):
        self.item = item
        self.parent = None
        self.left = None
        self.right = None
        self.color = 1

class RedBlackTree():
    def __init__(self):
        self.TNULL = Node(0)
        self.TNULL.color = 0
        self.TNULL.left = None
        self.TNULL.right = None
        self.root = self.TNULL

    # 前序
    def pre_order_helper(self, node):
        if node != TNULL:
            sys.stdout.write(node.item + " ")
            self.pre_order_helper(node.left)
            self.pre_order_helper(node.right)

    # 中序
    def in_order_helper(self, node):
        if node != TNULL:
            self.in_order_helper(node.left)
            sys.stdout.write(node.item + " ")
            self.in_order_helper(node.right)

# 后根
    def post_order_helper(self, node):
        if node != TNULL:
            self.post_order_helper(node.left)
            self.post_order_helper(node.right)
            sys.stdout.write(node.item + " ")

    # 搜索树
    def search_tree_helper(self, node, key):
        if node == TNULL or key == node.item:
            return node

        if key < node.item:
            return self.search_tree_helper(node.left, key)
        return self.search_tree_helper(node.right, key)

    # 删除后平衡树
    def delete_fix(self, x):
        while x != self.root and x.color == 0:
            if x == x.parent.left:
                s = x.parent.right
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.left_rotate(x.parent)
                    s = x.parent.right

                if s.left.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.right.color == 0:
                        s.left.color = 0
                        s.color = 1
                        self.right_rotate(s)
                        s = x.parent.right

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.right.color = 0
                    self.left_rotate(x.parent)
                    x = self.root
            else:
                s = x.parent.left
                if s.color == 1:
                    s.color = 0
                    x.parent.color = 1
                    self.right_rotate(x.parent)
                    s = x.parent.left

                if s.right.color == 0 and s.right.color == 0:
                    s.color = 1
                    x = x.parent
                else:
                    if s.left.color == 0:
                        s.right.color = 0
                        s.color = 1
                        self.left_rotate(s)
                        s = x.parent.left

                    s.color = x.parent.color
                    x.parent.color = 0
                    s.left.color = 0
                    self.right_rotate(x.parent)
                    x = self.root
        x.color = 0

    def __rb_transplant(self, u, v):
        if u.parent == None:
            self.root = v
        elif u == u.parent.left:
            u.parent.left = v
        else:
            u.parent.right = v
        v.parent = u.parent

    # 节点删除
    def delete_node_helper(self, node, key):
        z = self.TNULL
        while node != self.TNULL:
            if node.item == key:
                z = node

            if node.item <= key:
                node = node.right
            else:
                node = node.left

        if z == self.TNULL:
            print("Cannot find key in the tree")
            return

        y = z
        y_original_color = y.color
        if z.left == self.TNULL:
            x = z.right
            self.__rb_transplant(z, z.right)
        elif (z.right == self.TNULL):
            x = z.left
            self.__rb_transplant(z, z.left)
        else:
            y = self.minimum(z.right)
            y_original_color = y.color
            x = y.right
            if y.parent == z:
                x.parent = y
            else:
                self.__rb_transplant(y, y.right)
                y.right = z.right
                y.right.parent = y

            self.__rb_transplant(z, y)
            y.left = z.left
            y.left.parent = y
            y.color = z.color
        if y_original_color == 0:
            self.delete_fix(x)

    # 插入后平衡树
    def fix_insert(self, k):
        while k.parent.color == 1:
            if k.parent == k.parent.parent.right:
                u = k.parent.parent.left
                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.left:
                        k = k.parent
                        self.right_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.left_rotate(k.parent.parent)
            else:
                u = k.parent.parent.right

                if u.color == 1:
                    u.color = 0
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    k = k.parent.parent
                else:
                    if k == k.parent.right:
                        k = k.parent
                        self.left_rotate(k)
                    k.parent.color = 0
                    k.parent.parent.color = 1
                    self.right_rotate(k.parent.parent)
            if k == self.root:
                break
        self.root.color = 0

    # Printing the tree
    def __print_helper(self, node, indent, last):
        if node != self.TNULL:
            sys.stdout.write(indent)
            if last:
                sys.stdout.write("R----")
                indent += "     "
            else:
                sys.stdout.write("L----")
                indent += "|    "

            s_color = "RED" if node.color == 1 else "BLACK"
            print(str(node.item) + "(" + s_color + ")")
            self.__print_helper(node.left, indent, False)
            self.__print_helper(node.right, indent, True)

    def preorder(self):
        self.pre_order_helper(self.root)

    def inorder(self):
        self.in_order_helper(self.root)

    def postorder(self):
        self.post_order_helper(self.root)

    def searchTree(self, k):
        return self.search_tree_helper(self.root, k)

    def minimum(self, node):
        while node.left != self.TNULL:
            node = node.left
        return node

    def maximum(self, node):
        while node.right != self.TNULL:
            node = node.right
        return node

    def successor(self, x):
        if x.right != self.TNULL:
            return self.minimum(x.right)

        y = x.parent
        while y != self.TNULL and x == y.right:
            x = y
            y = y.parent
        return y

    def predecessor(self,  x):
        if (x.left != self.TNULL):
            return self.maximum(x.left)

        y = x.parent
        while y != self.TNULL and x == y.left:
            x = y
            y = y.parent

        return y

    def left_rotate(self, x):
        y = x.right
        x.right = y.left
        if y.left != self.TNULL:
            y.left.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.left:
            x.parent.left = y
        else:
            x.parent.right = y
        y.left = x
        x.parent = y

    def right_rotate(self, x):
        y = x.left
        x.left = y.right
        if y.right != self.TNULL:
            y.right.parent = x

        y.parent = x.parent
        if x.parent == None:
            self.root = y
        elif x == x.parent.right:
            x.parent.right = y
        else:
            x.parent.left = y
        y.right = x
        x.parent = y

    def insert(self, key):
        node = Node(key)
        node.parent = None
        node.item = key
        node.left = self.TNULL
        node.right = self.TNULL
        node.color = 1

        y = None
        x = self.root

        while x != self.TNULL:
            y = x
            if node.item < x.item:
                x = x.left
            else:
                x = x.right

        node.parent = y
        if y == None:
            self.root = node
        elif node.item < y.item:
            y.left = node
        else:
            y.right = node

        if node.parent == None:
            node.color = 0
            return

        if node.parent.parent == None:
            return

        self.fix_insert(node)

    def get_root(self):
        return self.root

    def delete_node(self, item):
        self.delete_node_helper(self.root, item)

    def print_tree(self):
        self.__print_helper(self.root, "", True)


if __name__ == "__main__":
    bst = RedBlackTree()

    bst.insert(55)
    bst.insert(40)
    bst.insert(65)
    bst.insert(60)
    bst.insert(75)
    bst.insert(57)

    bst.print_tree()

    print("\nAfter deleting an element")
    bst.delete_node(40)
    bst.print_tree()