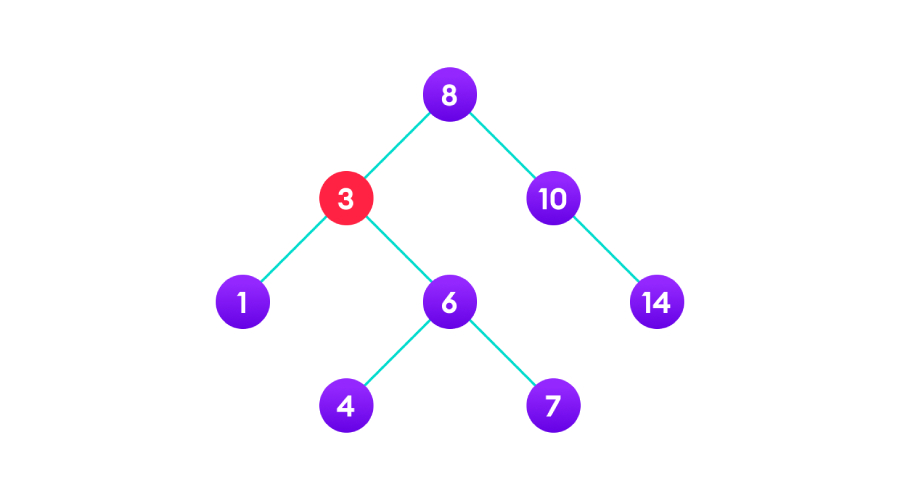
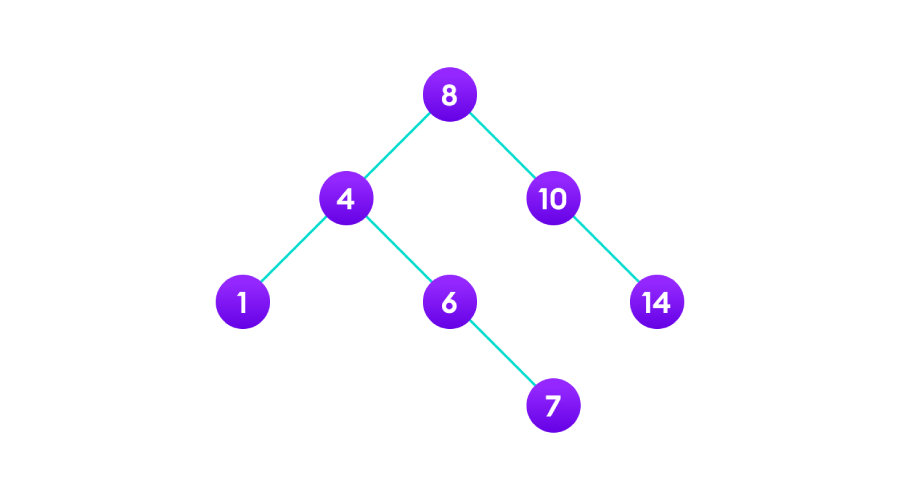
二叉搜索树(BST)左子树的所有节点都小于根节点,而右子树的所有节点都大于根节点,并且每个节点的2个子树也都是二叉搜索树。
二叉搜索树基本操作:搜索、插入、删除
搜索操作
搜索操作取决于二叉搜索树属性,如果该值低于根,我们可以确定该值不在右子树中,只需要在左子树中搜索;如果值高于根,可以确定该值不在左子树中,我们只需要在右子树中搜索。
算法:
If root==NULL
return NULL
If number==root->data
return root->data
If number<root->data
return search(root->left)
If number>root->data
return search(root->right)算法流程,以下图为例:
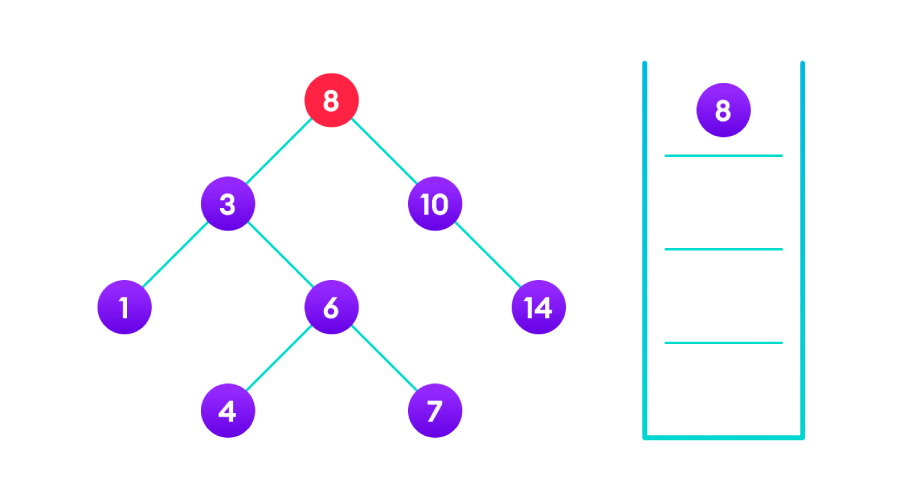
我们在二叉树中搜索“4”,因为根为8,8>4所以从左侧子树开始遍历;当根为“3”时,3<4则遍历右侧子树;当根为“6”时,6>4则遍历左侧子树,就搜索到“4”。
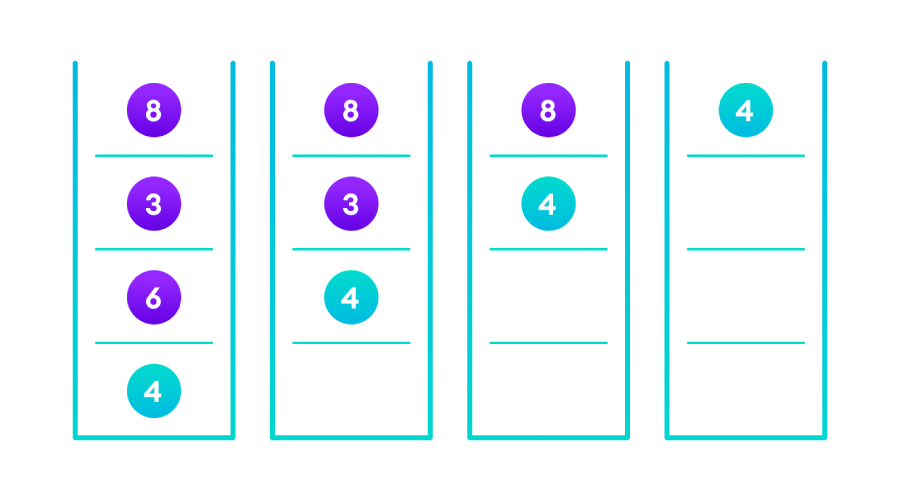
当返回新节点或NULL时,值会一次又一次地返回,直到搜索到目标,返回最终结果。如果最后还是找不到该值,会到达一个为NULL的叶节点,然后NULL会被返回。
插入操作
在为空节点插入一个值。根据左子树小于根,右子树大于根的规则。
按照二叉树结构值进行到右子树或左子树,当到达为空的节点时,将新节点的值插入。
算法:
If node==NULL
return createNode(data)if(data<node->data)
node->left=insert(node->left,data);else if(data>node->data)
node->right=insert(node->right,data);return node;算法流程,以下图为例:
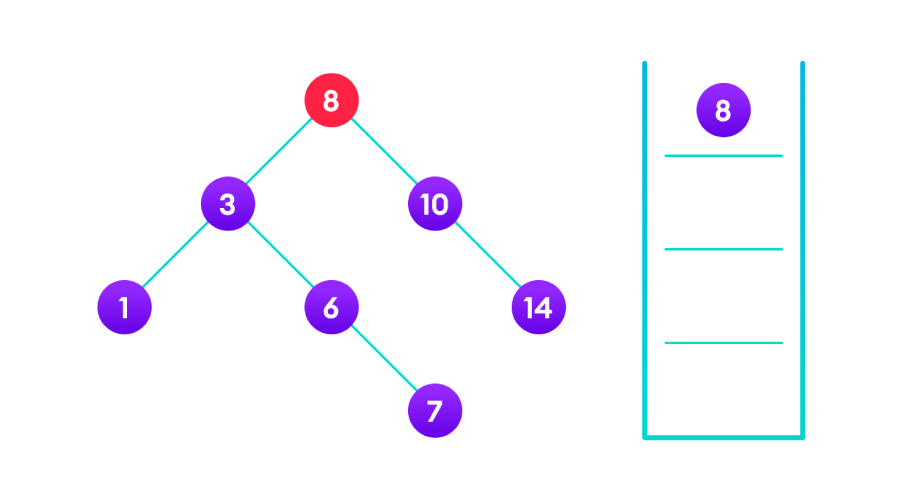
在二叉树中插入“4”,因为根为8,8>4所以到达左侧子树“3”;3<4则达到右侧子树“6”;6>4则到达左侧子树,因“6”的左侧子树为空,将“4”插入该节点,然后返回。
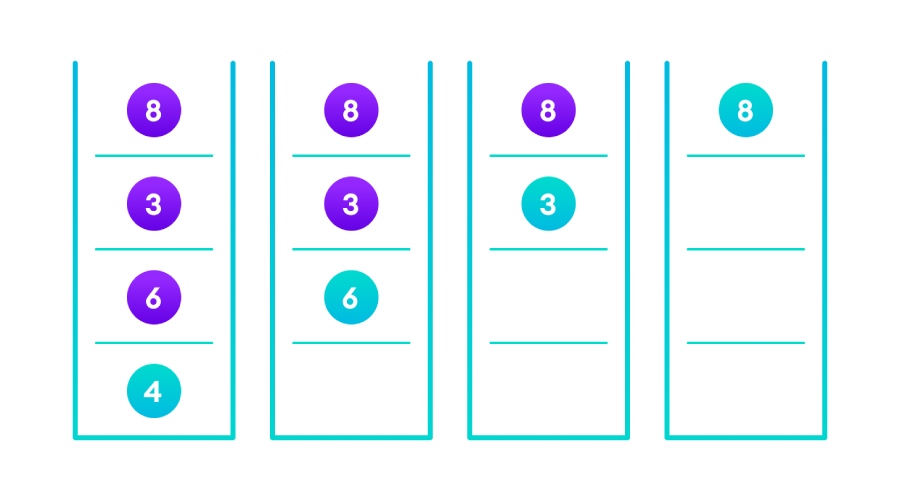
在NULL的情况下,返回新创建的节点并附加到父节点,否则返回相同的节点,直到我们返回根节点为止。
删除操作
情况1:删除子节点,只需从二叉树中找到节点删除即可。如下图:
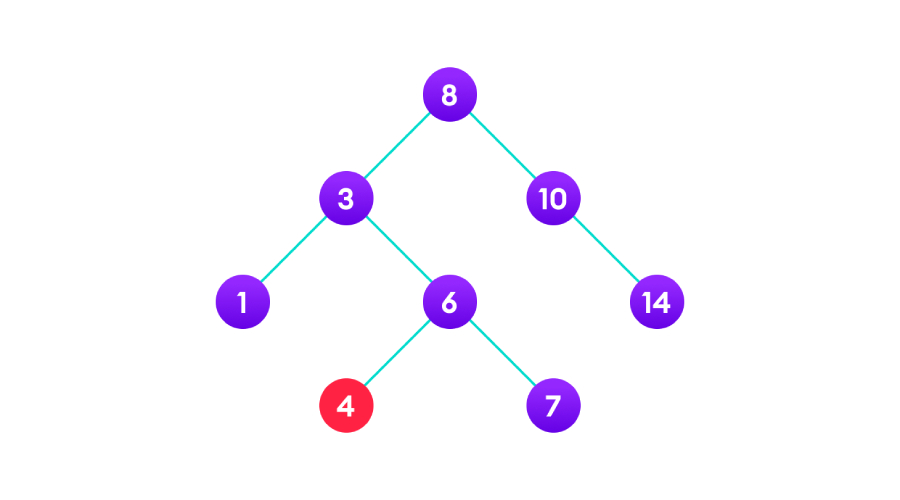
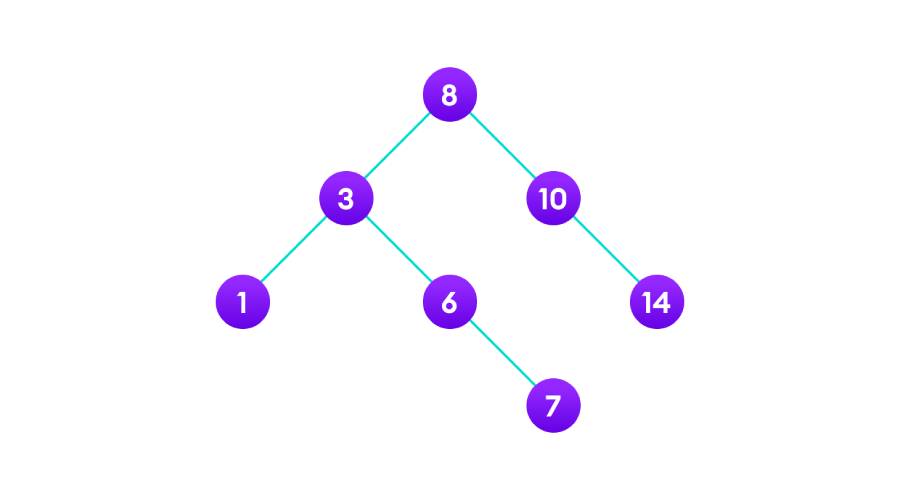
情况2:删除的目标节点有子节点。可以将目标节点替换为子节点或将目标节点删除。如下图:
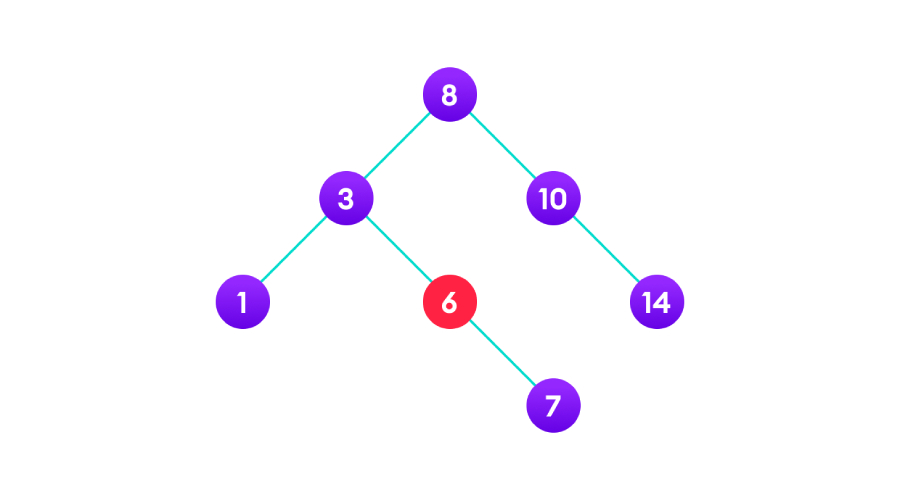
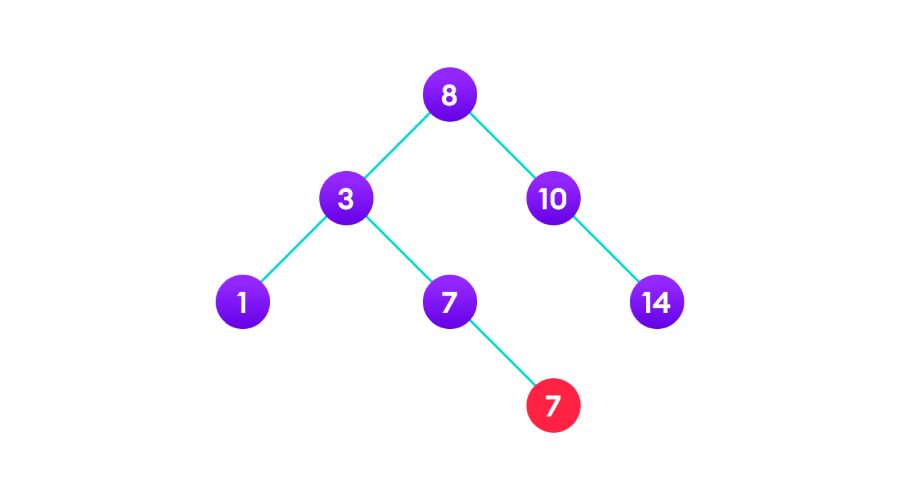
情况3:删除的目标节点有2个子节点。可以获取该节点的中序后继,用中序继任者替换节点,将顺序后继者从其原始位置移除。