前馈神经网络只允许信号从输入到输出以一种方式传播,没有反馈,是最简单的人工神经网络。基于可能存在的隐藏层,又可以进一步分类为单层或多层前馈神经网络。
前馈神经网络往往是将输入与输出相关联的简单神经网络,因为没有循环,其输出不会影响同一层。与神经网络的输出有关的层是输出层,它与隐藏层中的某些单元完全连接。前馈神经网络一般用于计算单个值,因此输出层只有一个单元和值。
前馈神经网络中的隐藏层
一个神经网络可以有多个隐藏层,但前馈神经网络通常只有一个隐藏层,隐藏层数越多,网络识别设计的能力就越高。
隐藏层中的每个单元通常与输入层中的某些单元完全连接。因为这个网络包含标准单元,所以隐藏层中的单元通过将每个输入的值乘以其相关权重、插入这些值并使用传递函数来计算它们的输出。
前馈神经网络的层数取决于功能的复杂性,通常是单向前向传播,权重在这里是静态的,激活函数由乘以权重的输入提供。为此,使用分类激活函数或阶跃激活函数。例如:如果神经元高于阈值(通常为0)并且神经元产生1作为输出,则神经元被激活。如果神经元低于阈值,则该神经元不被激活,阈值被视为-1。它们维护起来相当简单,并且能够处理包含大量噪声的数据。
前馈神经网络的应用
前馈神经网络的优势
- 不太复杂,易于设计和维护
- 单向传播,非常快速
- 对噪声数据高度敏感
前馈神经网络的缺点
由于缺乏密集层和反向传播,不能用于深度学习
前馈神经网络和反向传播算法的关系
反向传播算法在多层前馈神经网络上执行学习。通过输入为每个训练样本计算属性,输入被送入构成输入层的单元层。这些单元的加权输出同时馈送到第二层神经元,如称为隐藏层的单元。隐藏层是加权输出,可以输入到多个隐藏层等。隐藏层的数量可以看上述介绍。
最终隐藏层的加权输出是创建输出层的单元的输入,输出层扩散网络对提供样本的预测。隐藏层和输出层中的单元表示为神经元,因为它们具有象征性的生物元素或作为输出单元。通过隐藏单元提供的线性阈值函数的多层前馈网络几乎可以逼近某些函数。
前馈神经网络中的函数
1.代价函数
在前馈神经网络中,成本函数起着重要作用。分类数据点几乎不受权重和偏差的微小调整的影响。因此,可以使用平滑的成本函数来确定调整权重和偏差以提高性能的方法。
以下是均方误差成本函数:
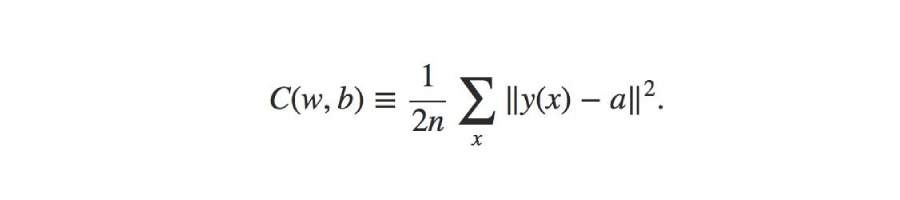
w是网络中收集的权重;b是偏差;n是训练输入的数量;a是输出向量;x是输入;‖v‖是向量v的正常长度。
2.损失函数
神经网络的损失函数用于确定是否需要在学习过程中进行调整。输出层中的神经元数等于类别数。显示预测和实际概率分布之间的差异。以下是二元分类的交叉熵损失:
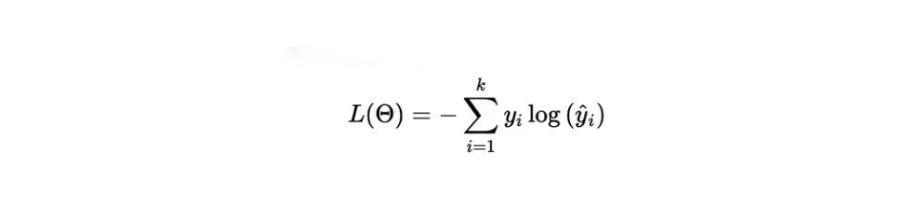
前馈神经网络的意义在于可以训练数据拟合自定义曲线来训练神经网络,以损失最小化为指导来实现参数内核和偏差的优化。





