模拟退火(SA),一种流行的优化模型参数的算法。基于现实生活中的物理退火原理,物理退火是加热材料达到退火温度然后缓慢冷却以将材料改变为所需结构的过程。当材料受热时,分子结构较弱,更容易发生变化;当材料冷却时,分子结构更硬,更不易改变。
模拟退火(SA)模拟物理退火过程,但是用于优化模型中的参数。这个过程对于存在大量局部最小值的情况非常有用。
模拟退火算法步骤
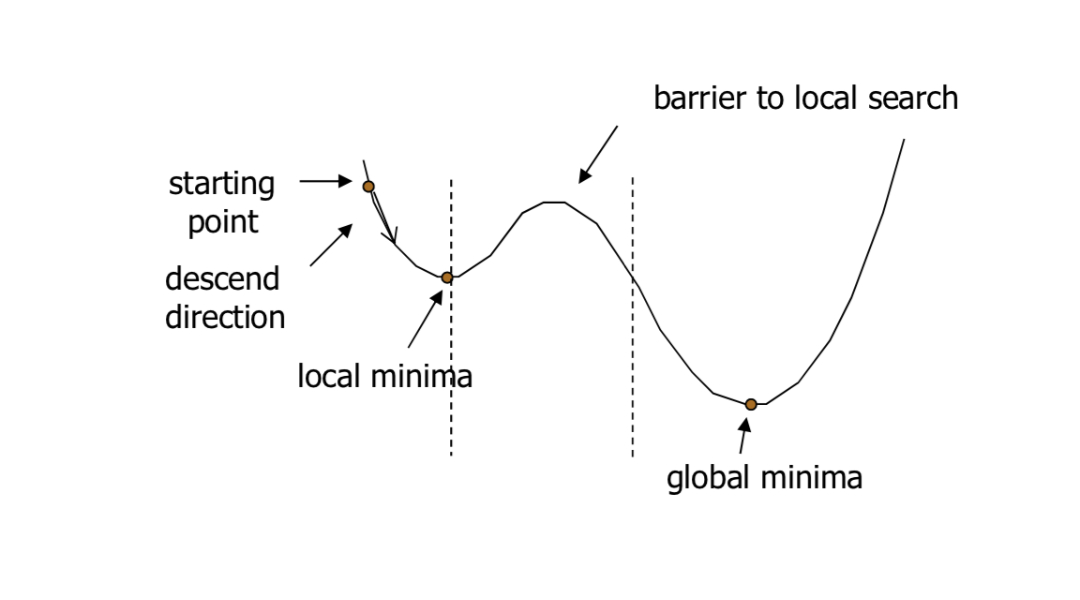
步骤1:我们首先从初始解s=S₀、初始温度t=t₀开始。
步骤2:设置降温函数alpha。通常有3种主要的降温规则:
1线性缩减规则:t=t-a
2几何缩减规则:t=t*a
3缓慢下降规则:t=t/(1+βt)
每个降低规则以不同的速率降低温度,并且每种方法都更适合优化不同类型的模型。对于第三条规则,β是一个任意常数。
步骤3:从初始温度开始,循环执行步骤4的n次迭代,然后根据alpha降低温度。停止此循环,直到达到终止条件。终止条件可能是达到某个结束温度,达到给定参数集的某个可接受的性能阈值等。时间与温度的映射以及温度下降的速度称为退火时间表.
步骤4:给定解决方案N(s)的邻域,选择其中一个解决方案并计算旧解决方案和新邻居解决方案之间的成本差异。解的邻域是所有接近解的解。例如,一组5个参数的邻域可能是如果我们要更改五个参数中的一个但保持其余四个相同。
步骤5:如果新旧方案的成本差异大于0(新方案更好),则接受新方案。如果成本差异小于0(旧解决方案更好),则生成一个介于0和1之间的随机数,如果它低于从之前的能量幅度方程计算的值,则接受它。
在模拟退火情况下,方程更改为:
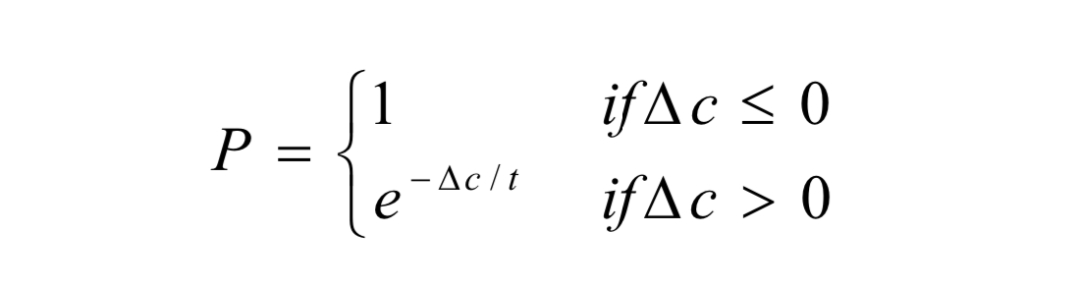
其中delta c是成本变化,t是当前温度。
在这种情况下计算的P是我们应该接受新解决方案的概率。
模拟退火(SA)算法优化问题示例
旅行商问题(TSP)
调度问题
任务分配
图着色和分区
非线性函数优化
模拟退火(SA)的优点与缺点
优点:易于实施和使用;为各种问题提供最佳解决方案。
缺点:如果退火计划很长,可能需要很长时间才能运行;算法中有很多可调参数。




