多元线性回归是最常见的线性回归形式。多元线性回归基本上描述了单个响应变量Y如何线性依赖于多个预测变量。
可以使用多重回归的应用示例:
1、房子的售价可能取决于位置的可取性、卧室的数量、浴室的数量、房子的建造年份、地块的面积以及许多其他因素。
2、孩子的身高取决于母亲的身高、父亲的身高、营养和环境因素。
多元线性回归模型参数
考虑一个具有k个独立预测变量x1、x2……、xk和一个响应变量y的多元线性回归模型。
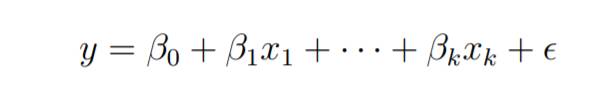
假设我们对k+1个变量有n个观测值,并且n的变量应该大于k。
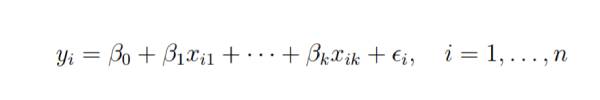
最小二乘回归的基本目标是将超平面拟合到(k+1)维空间中,以最小化残差平方和。
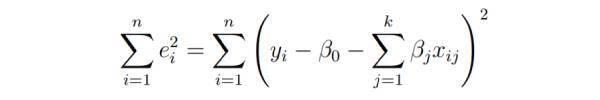
在对模型参数求导之前,将它们设置为零并导出参数必须满足的最小二乘法线方程。
这些方程是在向量和矩阵的帮助下制定的。

线性回归模型的写法如下:
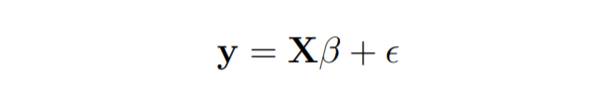
在线性回归中,最小二乘参数估计b
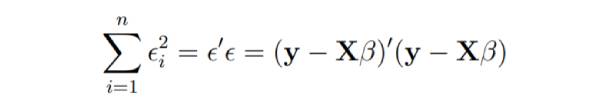
想象X的列是固定的,它们是特定问题的数据,并且说b是可变的。我们希望找到残差平方和最小化的“最佳”b。
平方和可能为零的最小值。
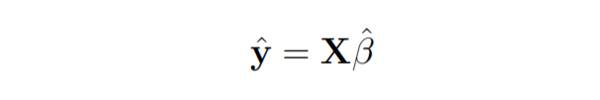
这里y是估计的响应向量。
代码在数据集data2上实现多元线性回归
data2数据集
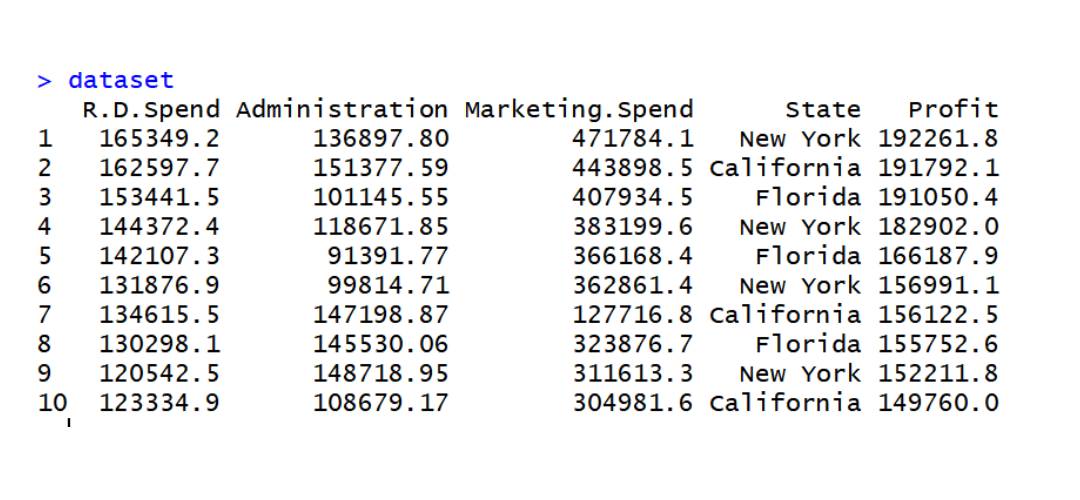
dataset=read.csv('data2.csv')
dataset$State=factor(dataset$State,
levels=c('New York','California','Florida'),
labels=c(1,2,3))
dataset$State
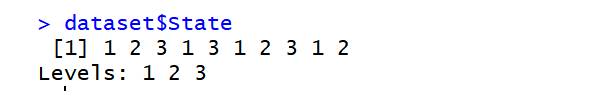
library(caTools)
set.seed(123)
split=sample.split(dataset$Profit,SplitRatio=0.8)
training_set=subset(dataset,split==TRUE)
test_set=subset(dataset,split==FALSE)
regressor=lm(formula=Profit~.,
data=training_set)
y_pred=predict(regressor,newdata=test_set)



