熵表示事件的不确定性大小,在数据科学领域,两个离散概率分布之间的交叉熵与KL散度相关,这是一个衡量两个分布相似程度的指标。在机器学习算法中,为了预测分布与真实分布有多接近,就可以通过交叉熵损失来判断。
给定真实分布t和预测分布p,它们之间的交叉熵由以下等式给出:
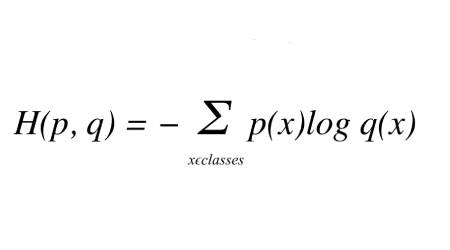
其中p(x)是真实概率分布(one-hot),q(x)是预测概率分布。
然而,在现实世界中,预测值与实际值不同,称为发散,因为它与实际值不同或背离。因此,交叉熵是熵和KL散度(散度类型)的总和。
现在让我们使用分类示例了解交叉熵如何适合深度神经网络范例。
每个分类案例都有一个已知的类别标签,其概率为1.0,而其他每个标签的概率为0。在此,模型确定特定案例属于每个类别名称的概率。然后可以使用交叉熵来确定每个标签的神经通路有何不同。
将每个预测的类别概率与所需输出0或1进行比较。计算出的分数/损失根据与预期值的距离来惩罚概率。惩罚是对数的,对于接近于1的显著差异产生较大的分数,而对于接近于0的微小差异产生较小的分数。
在训练期间调整模型权重时使用交叉熵损失,其目的是最小化损失——损失越小,模型越好。







