准确性指标计算模型在整个数据集中做出正确预测的次数。仅当数据集是类平衡的时,这才是可靠的指标,也就是说,数据集的每一类都有相同数量的样本。然而,现实世界的数据集严重失衡,通常使该指标不可行。而F1分数作为一种更加全面完善的机器学习评估指标,现已被大量用于衡量模型的准确性。
F1分数概念
说到F1分数就不得不了解混淆矩阵,混淆矩阵定义用于评估分类器的各种指标——准确度、精确度、召回率和F1分数,而F1分数结合了模型的精确度和召回率。
精度衡量模型做出的“积极”预测中有多少是正确的。
召回率测量数据集中存在的正类样本中有多少被模型正确识别。
准确率和召回率提供了一种权衡,即一个指标以另一个为代价。更高的精度涉及更严格的分类器,怀疑数据集中的实际正样本,从而降低召回率。另一方面,更高的召回率需要一个松懈的分类器,它允许任何类似于正类的样本通过,这使得border-case负样本被归类为“正类”,从而降低了精度。理想情况下,我们希望最大化精度和召回率指标以获得完美的分类器。
F1分数使用它们的调和平均值结合精确度和召回率,最大化F1分数意味着同时最大化精确度和召回率。
如何计算F1分数?
要理解F1分数的计算,首先需要认识混淆矩阵。上文我们提到F1分数是根据精确度和召回率定义的。其公式如下:
精度

召回率
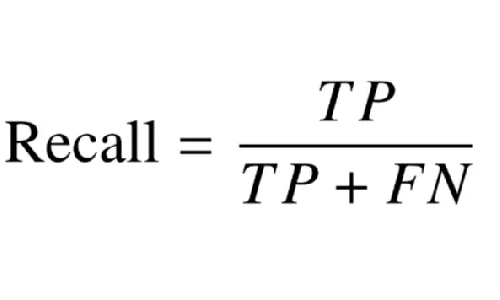
F1分数计算为精度和召回分数的调和平均值,如下所示。它的范围为0-100%,较高的F1分数表示更好的分类器质量。
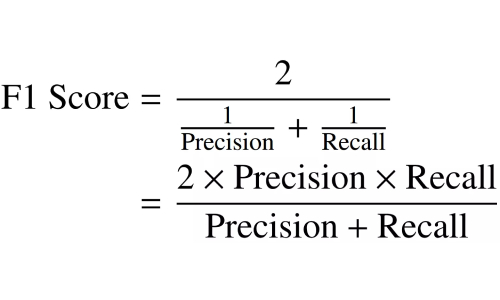
调和平均值鼓励相似的精确率和召回率值。也就是说,精确率和召回率彼此偏离得越多,调和平均值就越差。
就混淆矩阵的四个基本元素而言,通过替换上式中精度和召回率的表达式,F1分数也可以写成:
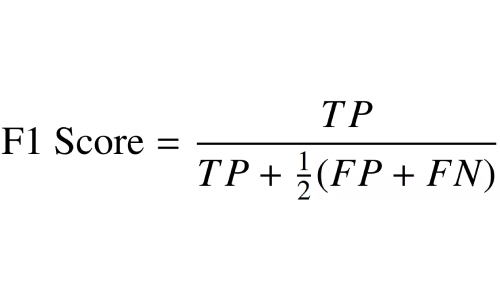
为了计算多类数据集的F1分数,使用了一对一技术来计算数据集中每个类的个体分数。取类精度和召回值的调和平均值。然后使用不同的平均技术计算净F1分数。
宏观平均F1分数

模型的宏观平均F1分数只是获得的类F1分数的简单平均值。只有当使用的数据集在其每个类别中具有相同数量的数据点时,宏平均F1分数才有用。然而,大多数现实世界的数据集都是类别不平衡的——不同的类别有不同数量的数据。在这种情况下,简单的平均值可能会误导性能指标。
微平均F1分数

微平均F1分数是一种对多类数据分布有意义的指标。它使用“净”TP、FP和FN值来计算指标。
净TP是指数据集的类TP分数的总和,它是通过将混淆矩阵分解为对应于每个类的one-vs-all矩阵来计算的。
样本加权F1分数

样本加权F1分数非常适合计算类不平衡数据分布的净F1分数。顾名思义,它是类F1分数的加权平均值,其权重由该类中可用的样本数决定。
Fβ分数
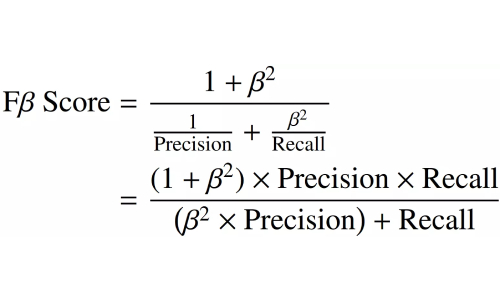
Fβ分数是F1分数的通用版本。它计算调和平均值,就像F1分数一样,但优先考虑精度或召回率。“β”表示权重系数,该系数是用户设置的超参数,始终大于0。







