共轭梯度是一种求解线性方程组数值解的算法。共轭梯度法通常以迭代算法的形式实现。共轭梯度法也可以用来解决无约束的优化问题。
简单描述共轭梯度算法
共轭梯度算法的优势就是每个方向都走到了极致,也即是说寻找极值的过程中绝不走已经走过的方向,比如说求n空间的函数极值走n步就解决了。
实例求解线性方程的共轭梯度
线性方程Ax=b,其中A是n×n对称正定矩阵,x和b是n×1向量。求解这个方程的x相当于下面的凸函数f(x)的最小化问题
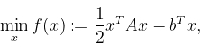
迭代地求解x的Ax=b,定义残差r(x):=∇f(x)=Ax−b。
然后再迭代xₖ,我们有
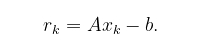
f沿xₖ+αpₖ的一维最小化器明确给出(通过将f(xₖ+αpₖ)wrtα的一阶导数设置为零)如下

在共轭梯度法中,方向集{p₀,p₁,…}的选择使得其元素关于A是共轭的,即
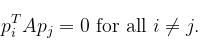
每个方向pₖ被选择为负残差-rₖ(这是函数f的最陡下降方向)和前一个方向pₖ-₁的线性组合。我们写
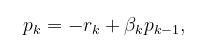
其中标量βₖ由pₖ-1和pₖ必须关于A共轭的要求确定。通过将最后一个方程预乘以
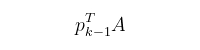
并施加条件
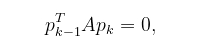
我们发现
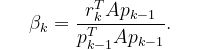
知道αₖ和pₖ,下一次迭代可以像往常一样使用

如前所述,方向集{p₀,p₁,...}的选择使其元素相对于A是共轭的。
但是我们如何选择第一个搜索方向p₀呢?只需在初始点x₀使用良好的ol'最陡下降方向,即p₀=-r₀。
由此得出该线性方程的共轭梯度工作算法(撇号表示转置操作):
Initialize x₀
Calculate r₀=Ax₀−b
Assign p₀=−r₀
For k=0,1,2,…:
*calculateαₖ=-rₖ'pₖ/pₖ'Apₖ
*update xₖ₊₁=xₖ+αₖpₖ
*calculate rₖ₊₁=Axₖ₊₁-b
*calculateβₖ₊₁=rₖ₊₁'Apₖ/pₖ'Apₖ
*update pₖ₊₁=-rₖ₊₁+βₖ₊₁pₖ



