k最近邻算法是为了识别给定查询点的最近邻,进而将这些数据进行分类。而且k最近邻算法严重依赖已存储的训练数据,因此也称为基于实例或基于内存的机器学习算法。
k最近邻算法可以用于分类或是回归问题的处理,处理分类问题时用离散值,而处理回归问题用连续值。在进行分类之前,必须定义距离,主流的距离度量有这几种。
欧几里得距离
这是最常用的距离度量,仅限于实值向量。使用下面的公式,它测量查询点和被测量的另一个点之间的直线。
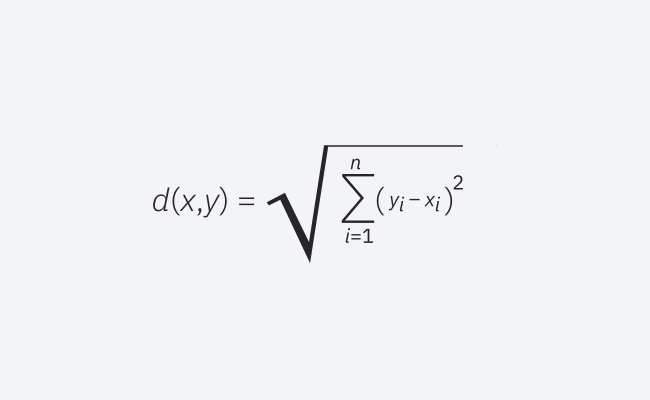
欧几里得距离公式
曼哈顿距离
这也是一种流行的距离度量,它测量两点之间的绝对值。

曼哈顿距离公式
闵可夫斯基距离
此距离度量是欧几里德和曼哈顿距离度量的广义形式。

闵可夫斯基距离公式
汉明距离
该技术通常与布尔或字符串向量一起使用,识别向量不匹配的点。因此,它也被称为重叠度量。

汉明距离公式
确定k最近邻算法距离的意义
为了确定哪些数据点最接近给定查询点,需要计算查询点与其他数据点之间的距离。这些距离度量有助于形成决策边界,将查询点划分为不同的区域。







