Fenwick树基本原理 二叉索引树实例

Fenwick树又名二叉索引树，是一种数据结构，可以有效地计算数组的前缀和。

前缀和本质上是一组数字的运行总和。

例如，已知一个数组是[2,3,-1,0,6]，求长度为3的前缀和，那么就是[2,3,-1]的数组和2+3-1=4。

有效计算前缀总和在很多情况下都很有用。

二叉索引树的基本原理

我们知道每个整数都可以用2的幂次方表示。类似地，对于大小为N的给定数组，我们可以用数组BIT[]表示，这样在任何索引处，我们都可以存储给定数组的数字和。

举个例子

int a[]={0,1,2,3,4,5,6,7,8,9,10,11,12,13,14,15,16};

下图是二叉索引树，其中每个封闭的框表示值BIT[index]，每个BIT[index]存储一些数字的部分和。

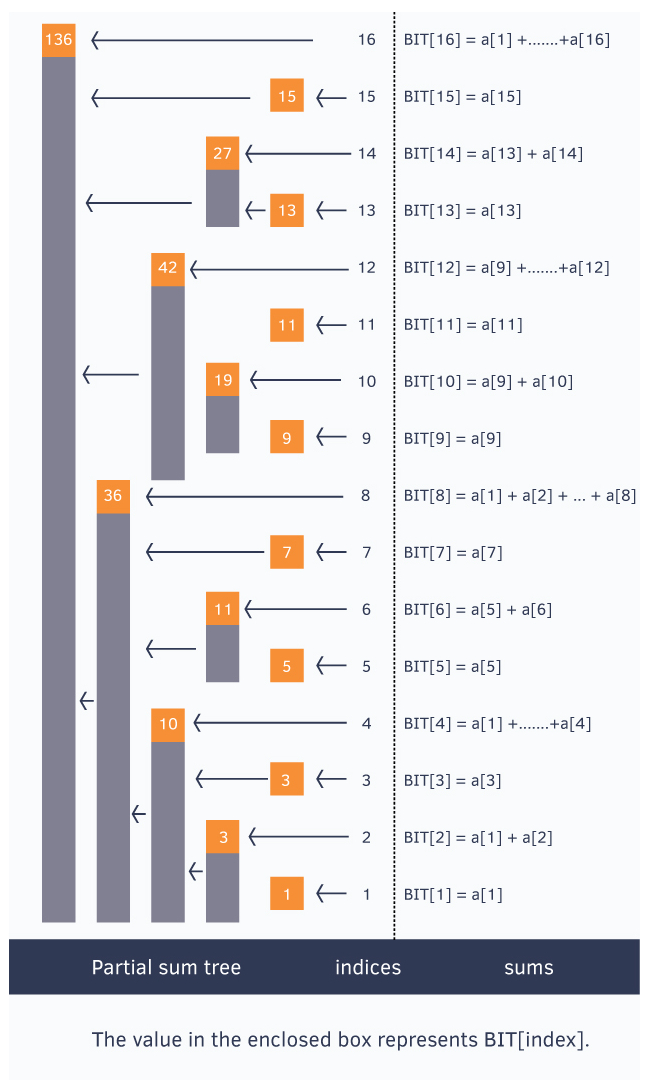
注意

{a[x],X是奇数
BIT[x]=a[1]+...+a[x],X是偶数
}

为了概括这一点，BIT[]数组中的每个索引i存储从索引i到i-(1<<r)+1（包括两个值）的累积和，其中r表示索引i中的最后一个设置位

数组a[]中前12个数字的总和=BIT[12]+BIT[8]=(a[12]+…+a[9])+(a[8]+…+a[1])

同样，前6个元素的总和=BIT[6]+BIT[4]=(a[6]+a[5])+(a[4]+…+a[1])

前8个元素的总和=BIT[8]=a[8]+…+a[1]

BIT[]是一个大小=1+需要对其执行操作的给定数组a[]的大小的数组。最初BIT[]中的所有值都等于0。然后我们为给定数组的每个元素调用update()操作来构造二叉索引树。

void update(int x,int delta)
{
for(;x<=n;x+=x&-x)
BIT[x]+=delta;}