AVL树是一种平衡二叉搜索树,其特点是左侧子树与右侧子树的高度差的绝对值是0和1。
AVL树实例图
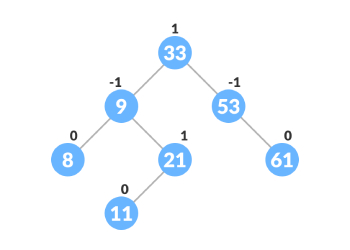
AVL树旋转、插入、删除操作
1、AVL树旋转子树
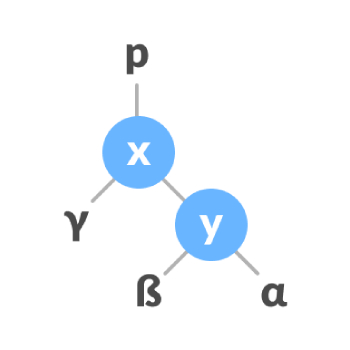
即交换子树节点的位置,旋转后的AVL树依旧遵循高度平衡规则。左旋转,右侧节点的排列被转换为左侧节点的排列。前后如下图:
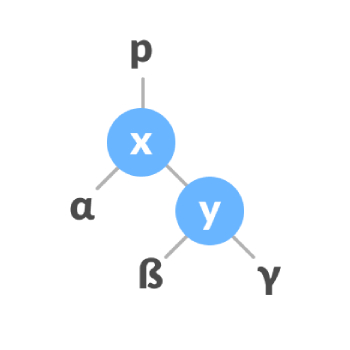
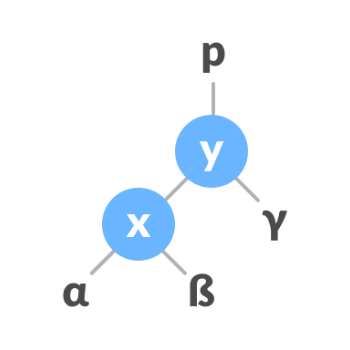
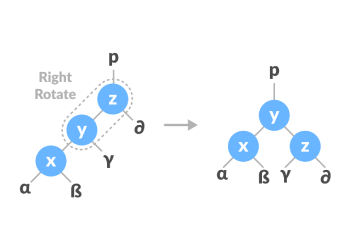
右旋转,左侧节点的排列被转换为右侧节点的排列。前后如下图:
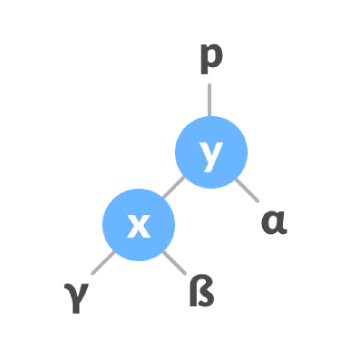
平衡旋转,有2种情况,一是先左旋转后右旋转,排列首先向左移动,再向右移动;二是先右旋转再左旋转,排列首先向右移动,再向左移动。如下图:
先左旋转后右旋转。
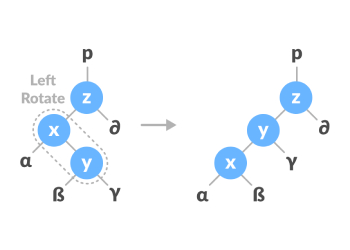
先右旋转再左旋转。
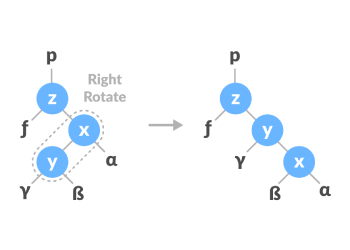

2、插入新节点
初始二叉树。
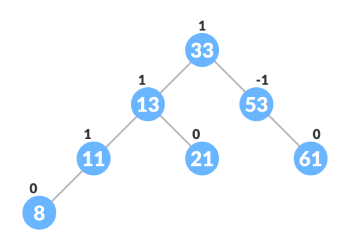
设要插入的节点“9”,首先遍历初始二叉树左侧子树和右侧子树,再考虑AVL树高度平衡规则,则得出最后的二叉树结构,如下图:
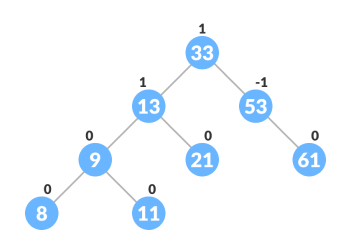
3、删除节点
删除节点后,AVL树的平衡发生变化。为了重新平衡,需要执行适当的旋转。
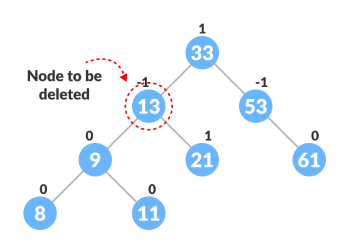
首先,定位要删除的节点,根据节点是否存在子节点,进行替换删除,考虑高度平衡规则,需要旋转来平衡。
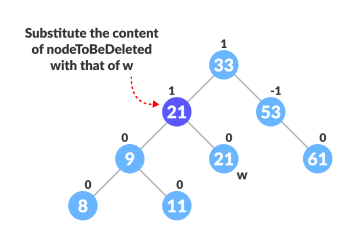
替换要删除的节点。
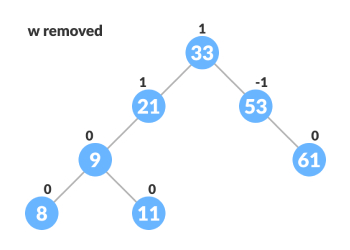
删除节点W,并更新。
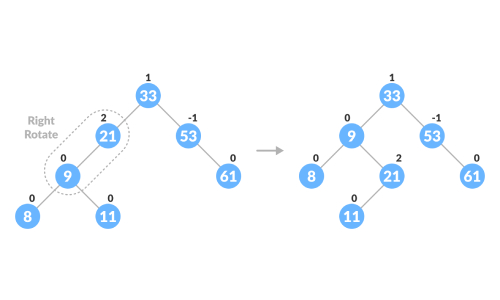
向右旋转以平衡树。
最终得到Avl树,如下图:















